Bias Variance Tradeoff

Imagine you have developed a model that predicts the total number of runs in a cricket match. You have utilized all the possible stats from previous Cricket world cup and you are getting near perfect results on training data. Excited by these early results you bet on tonights match to check how many runs each team makes… but you totally miss the score board.

How did this happen? To answer that, it’s helpful to understand the tradeoff between the two main types of reducible model error: bias and variance.

Let’s see what excatly is the model error?

Model error is basically a sum of three parts.

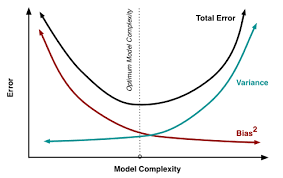
\[Total Error = Irreduciable Error + Bias Error + Variance Error\]

In an an ideal model you would seek to minimize bias and variance. But as the word tradeoff suggests, its not that simple.

The Bias-Variance tradeoff is a basic yet important concept in statistics and machine learning.But what does bias and variance actually mean and how are they related to the accuracy and performance of the model?

Bias

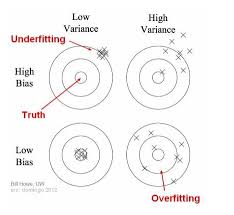
Bias is the same as the mean square error (MSE). It is the inability of a model to learn enough about the relationship between predictor \(X\) and the response \(Y\). Models with high bias tend to underfit the training data, creating a high training error, and oversimplify the relationship between the predictors and the response.

In mathematical term, for some test point \(X_o\) the bias of \(Y_o\) is given by,

\[Bias[Y_0]=E[Y_0]-f(X_0)\]

Now lets get back to our cricket match, suppose the goal of your model is to predict the total number of runs from overall batting average of the team.Let’s caveat that a team’s number of runs scored increases with its batting average, but gradually plateaus. Fitting a linear model to estimate the curved “true” relationship between batting average and runs will result in a biased model, beacuse the model oversimplifies the true relationship with a straight line.At some batting averages, the model will tend to underestimate a team’s runs, and at other batting averages, the model will tend to overestimate them.

variance

In contrast, Variance shows how subject the model is to outliers, meaning those values that are far away from the mean.Variance qauntifies models tendencey to learn too much about the relationship that’s implied by the dataset. Models those with high variance tend to overfit. Meaning such models tend to go beyond the true signal into the noise. Such models tend to unnecessarily complicate the relationship between the predictors and the response, and therefore tend to generalize poorly to other datasets, consequently creating high test error. A good way to think about variance is that it represents a model’s lack of consistency across datasets.

In mathematical term, variance of the estimator at test point \(X_0\) is given by, \(Variance[Y_0]= E[(Y_0 -E[Y_0])^(2)]\)

If you fit a high-variance model with different datasets, the errors may not tend to over- or underestimate the response on average, but the model’s error at a specific point may change drastically depending on the data used for training.

Now suppose for our cricketing example we created a complex model which maps all the relationships from the dataset including all the noise and ourliers. Such model will fail to generalize the result and performs bad on unseen data.

Bias Variance Tradeoff

In an ideal scenario, we would be able to develop the perfect model using infinite training data, thereby eliminating all error due to bias and variance.In practice, however, its not always possible to get that much data thus, we must make trade-offs between simplifying the modeled relationship (reducing variance, but potentially introducing bias) and trying to capture more of it (reducing bias, but potentially introducing variance). Finding the sweet spot helps us minimize the model’s total overall error.

Understanding the trade-off between bias and variance can help you minimize overall error and train a model that generalizes appropriately. Identifying and reducing both bias and variance is vital to building a robust, high-performing model that solves your problem.